Previously, I described a general approach to solving Nonograms. I didn’t go into many details about the actual implementation. Here I go further, in an effort to win back some of the sunk cost involved in the development.
The Basics
The software was written in Python 2.4. There were around 700+/-300 lines, depending on how you count and who’s asking.
For debugging purposes, I used the Python Imaging Library and PyGame.
Much of mapping from the general approach to the specific Python was fairly straightforward. Of course, it had all the typical bugs, and it took the mandated “twice as long as I expected”. Apart from the standard gripes, there is nothing to blog home about.
My standard gripes with Python include:
-
Wasted time correcting inconsistent case in identifiers. (False != false) == True!
-
Similarly, spelling errors in variable names are detected very late early in late-binding languages like Python, despite being, by far, the most common mistake I make. It is frustrating to take over 30 seconds to detect this type of error.
-
It’s not Python’s fault but I change programming languages frequently enough to forget the basic syntax. (Does “.” or “+” concatenate strings? Is an equality test “=” or “==”? Do you add, insert or push an item into a set?)
-
IDLE, the free IDE with Python, is missing a stack of fairly basic features:
-
Don’t just show me an error message! Take me to the line that it occurs on!
-
Unindent is a clumsy word, but a critical feature.
-
Recursion versus Iteration
The high-level approach described had pixels notifying segments of changes to constraints that in turn notified other pixels, recursively. I factored out this recursion, and replaced it with iteration. This was an important implementation decision that differed from my previous Sudoku-solving architecture, which was otherwise very similar.
To achieve this, I used the Command pattern to create a hierarchy of Command objects. A Command Dispatcher object accepted requests for commands to be executed, queued them up and then called the appropriate methods when it was triggered to do so.
This technique had several advantages and disadvantages:
-
Recursion is clean, pure and fun to think about, but iteration is generally faster.
That said, I have no evidence that this was the case here.
-
The main loop of the application was simple.
It was a simple case of “while the queue is not empty, call the command dispatcher.”
Having control return repeatedly to the main loop made it easy to instrument animation of the algorithm. The loop was modified to add a call to redraw the display (and manage any outstanding windows events). This would have been more difficult using the recursive algorithm.
-
It opened the possibility to change the ordering of commands. Similarly, it opened the possibility to discard commands.
I did implement a priority of commands – some types of commands would always be run before other types. That enforced an ordering that is necessary, with the current implementation to ensure that all the segment fields are initialised before being queried by the cells. In hindsight, with some refactoring, that could have been removed, leaving a simpler solution.
The biggest bang-for-buck optimisation would almost certainly be detecting that an identical command is listed twice in the queue and deleting one of them. For example, there is no reason to have two orders in the queue at the same time to tell a pixel to recalculate its colours. Once the first one is executed the second one is obsolete, until another segment requests it occur again.
Another possibility that I did not implement was to try to make the order of the processing seem “more natural” to a human observing the animation. By focussing the processing on, for example the top-left corner, before processing equivalent commands on the bottom-right, I thought it might make the puzzles solution tend to appear as a gradual, yet intermittent (perhaps the right word is “punctuated”?) wipe rather than the whole puzzle being gradually being brought into focus with a series of quick waves.
The downside of all of these optimisations is the encapsulation-leakage between the command dispatcher and the semantics of the commands themselves.
-
Debugging was tricky.
Often I would be debugging the execution of a command when I would realise the mistake was that the command was being run at all. In the recursion case, the context in which the decision to execute a method is still available, higher in the call stack (via the debugger or the call-stack dump in the case of an assertion). With iteration, the context which led to a command being called is lost – all that remains is the result of the decision being pushed on the command stack.
Animation
The use of an animated algorithm was a first for me.
I have used the Python Imaging Library a fair amount before. The image.show() method is very useful. It simply pops up a window containing an image. I have often used the image.show() method to get a quick look during at an algorithm’s progress during debugging (especially when working on image processing). However, repeated calls to it open different windows, and I have been caught out on several occasions, when I have forgotten to remove some debugging code. I have sent an application wildly creating dozens or hundreds of windows; each one needs to be individually closed. I resolved to work smarter this time, and had a look at PyGame again.
It took me about a dozen lines of code – and three or four tries at placing them in the right place – to get the infrastructure in place to animate my algorithm. On top of that, I needed to write some code that actually drew the pictures. Combined, the infrastructure requested an update of the image every time a command was completed, and updated the image on the screen. I could watch the puzzle being solved, giving some sense of progress (and a greater sense of despair when a bug caused it to go wrong!)
This is probably a lot of CPU overhead, but it ran faster than I had hoped. I put in a counter to only draw the picture every 100 commands. It sped it up by about an order of magnitude.
Animation Snapshots
Here are some pictures of the algorithm at work. Each cell in the grid is represented by a circle. Each circle is evenly divided into pie-slices, representing each of the colours it might be.
 |
7% complete | |
 |
50% complete | |
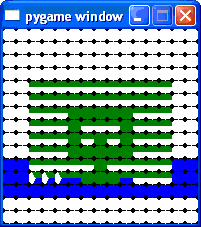 |
75% complete | |
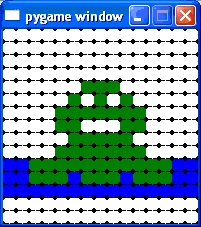 |
Nonogram completed after 5363 commands. |
Can you make out the completed image?
Try squinting.
It helps if you know the nonogram is named “Froggy”.
Here’s another image. This one was exciting because it was the first puzzle completed by the software that I didn’t solve first by hand.

STOP PRESS, 11-Aug-05: I finally got around to typing in the clues to a semi-large puzzle – 40×35, although I render this as 40×40 with five blank rows at the top. The software successfully solved it – albeit slowly!

Visual Debugging
After each run, when the algorithm had gone as far as it could, I let the application keep running, still processing the standard window-manager event loop. It didn’t take too long implement mouse-click detection in this loop. It would calculate which pixel had been selected and print out various debugging details, depending on the mouse button pressed. This turned out to be surprisingly effective at helping me narrow down the bug that had eluded me for the longest time beforehand. (I had neglected to ensure that the white segments at either end of the row were anchored to the edges, which was leading to the algorithm stalling.)
An area that could have been improved would be to have a graphical representation of the segments as well as the pixels. I didn’t come up with any ideas about how to easily present that, but it probably would have helped the debugging.
Q&A
Alastair made a comment on the previous post:
Object-oriented analysis is the real winner here.
This is an interesting point.
My first reaction was: No, my model wasn’t particularly pure OO, for a variety of reasons:
-
Python makes everything public, and leaving it to the developers’ sense-of-honour not to look at private data members and break encapsulation. For a casual project like this, I have little such sense-of-honour – especially for the debugging code which peered at data all over the place, and made assumptions about the internal behaviour of other classes. In a larger project with maintenance issues and witnesses, I would not have been so blasé.
-
While I did use inheritance, it was only for the Command design pattern – the main algorithm didn’t use it.
-
I also used a lot of set and list manipulation that felt awfully functional to me.
-
I didn’t even bother with a Model-View-Controller pattern. The pixel object knew how to draw itself. (Of course, some would argue that that is the Right WayTM.)
Then, I think I saw Alastair’s real point.
There was no overarching procedure “owning” the process – just lots of objects doing their small bit, understanding their own rules. Communication was done through messages being passed to each other without an understanding of what that might entail. The overall solution just bubbled up from the “hum of the parts”.
It is exciting to see emergent behaviour coming from objects this way. I recall a PhD student explaining to me many, many years ago how his English natural language parser worked in a similar way. Each word in the sentence tried to work out its place in the sentence (noun/verb/adjective, subject/object, etc.) with only reference to the attributes of its neighbouring words. There was no overall parser. It seemed indistinguishable from magic to me then; I wonder if this technique has passed the test of time.
I think the key benefit here of OO is to separate the task of modelling the rules of the puzzle from the task of solving it. Just curious whether you enforced this separation in the code itself?
I really wanted to answer “Yes” to this question. I tried to treat this question like a job-interview question. I wanted to produce an example showing I did exactly this, and it was in the back of my mind the whole time.
Unfortunately, I think the answer is: No, I took too many shortcuts.
Alastair also asks:
why [did] you chose the white segment maximum length to be the grid size, when it plainly could never get to this size? Does it affect your analysis if you put a more realistic upper limit on the white segment sizes (e.g. grid size minus coloured segment sizes at least)?
There are four parts to the answer.
-
The pedant in me says: Strictly, a white segment can take the whole row if there are no coloured segments at all on that row. Although this is a bit of a special-case, it does routinely appear in some puzzles, especially when someone is forcing a rectangular picture to appear in a traditional square nonogram.
-
The analyst in me says: No, it wouldn’t affect the analysis – in fact it would probably be a moderately powerful optimisation to limit the size of the white segment to the (grid Size – sum(coloured segment sizes)).
-
The purist in me says: Computing the size of the other segments on the row can’t be done by the segment – it has no visibility to most of the segments. It isn’t really the responsibility of the pixel, so the job would have to be done by an external object (perhaps a new Row object). Creating a whole entity to solve a problem that gets solved implicitly anyway seems needless.
-
The honest man inside says: The real reason I didn’t do it was laziness. Not doing it just meant waiting a bit longer for the solution to be found.
Comment by Alastair on June 12, 2005
Wow, thanks for such detailed answers.
You correctly interpreted my meaning behind the OO comment.
Comment by Nonograms lover on July 14, 2014
I’ve written a nonogram solver too, but in C++, where encapsulation is much easier to enforce. It’s actually the first step to write a program that can generate them.