The Puzzle Solver Framework
Regular readers will be familiar with my approach to puzzle-solving, and will remember a number of different puzzles that I automated in the past.
Back in January, I created a framework to solve these types of puzzles. At the time, I wrote in the conclusion:
It still needs some work, and the proof of a framework isn’t in the first application that uses it, but in the third, so I am not crowing about it too much yet.
Well, eight months later, I am one step closer to that, having used the framework to tackle the Circuit Game puzzle – the second application to use it.
The Game Objects
The key part to using the framework, is working out how the puzzle can be decomposed into individual objects.
Typically, these objects store a small amount of local state and references to the neighbourhood other similar objects they interact with. They also maintain a set of possible solution values. They are in charge of enforcing a simple set of constraints, whittling down the set of possible values until only one remains. Finally, they are responsible for letting their neighbours know about changes in their state, so the neighbours can correspondingly re-apply their constraints.
Thus, the constraints are propagated across neighbourhoods, peer-to-peer, with little or no oversight from over-arching objects.
Game Objects in the Circuit Game
In this puzzle, each square (or cell) represented a game object.
Each cell was responsible for maintaining its shape (e.g. Tee, Corner, etc.) This was implemented through a class hierarchy.
Each cell was responsible for tracking its four neighbours.
Each cell was also responsible for maintaining a list of compass directions and its disposition on whether or not a wire was exiting the cell in that direction. For each direction, the disposition could be that a wire must, must not or might be leaving the cell in that direction. Below, I describe how this was calculated.
For the subset of shapes that could be rotated (e.g. Corner, Line, Bulb, and Tee cells, but not Cross or Empty cells), each shape was responsible for maintaining the list of valid orientations.
By iterating through each of the valid orientations, and examining the resulting directions that the wires pointed, it was possible to mark the disposition of each compass direction. If all remaining orientations had a wire pointing up, then the disposition was must. If none of them did, it was must not. If some did, and some didn’t, it was might.
Each of the rotatable shapes were also responsible for maintaining the key constraint in the puzzle – that this cell’s disposition of a wire, was compatible with its neighbour’s disposition of the same wire.
For example, if my neighbour to the left thinks that there must be a wire pointing to its right (e.g. back to me), then I must have a wire pointing to my left. Any orientation of my shape that doesn’t correspond to that can be eliminated from consideration.
To simplify the bounds-checking, I surrounded the entire puzzle in a border of Empty Cells. These cells never contacted their neighbours, so they didn’t peer past the limit of the grid. That isn’t the most sophisticated of solutions for dealing with boundary conditions, but it worked.
Power/Cycles
As it stands, this only enforces the rules in Rotate2 (See the original article for the differences.)
I expected that I would need to implement a global property to enforce that there should be no cycles. This supports the concept of power cells.
I even had a comment in the code pointing out where such functionality would go.
In practice, I found that it wasn’t required to solve the puzzles that were posed by the web-sites.
In theory, there could exist a puzzle that this engine couldn’t solve, because it would see two possible ambiguous solutions (one false solution containing a cycle, and one without). In practice, I haven’t seen one. It remains an open challenge to come up with such a puzzle.
[Stop Press: It is no longer open]
Did it work?
I mentioned in the original article that these puzzles didn’t seem to have the complexity of Slitherlinks and the like. This was borne out in the run-time; these test puzzles I encoded were all solved by the engine in sub-second timeframes, even with basic graphical animation.
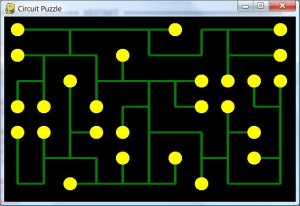
This is an example of a solved puzzle; this puzzle is the one shown in my original Circuit Puzzle article.
These puzzles can be crossed off the list as beaten.
How did the framework go?
I initially used the same version of the framework as the Alphametics puzzle. I found a couple of trivial bugs, with single character corrections, and made no changes to the interface.
I found it took me a little while to remember the concepts; I need to add some documentation to give me clues to get my head back into the right context to use it.
Related to that, I found that when I missed a tiny piece of necessary plumbing that my game objects were responsible for including, the whole object model just sat there. I couldn’t work out why nothing at all was happening – the framework couldn’t see that there was any work to do. I eventually added the missing line in, and the whole thing jumped to life.
The Command Queue which I spent so much pondering about in the past, was completely in the background. I didn’t give it a moment’s thought; the framework just took care of it.
So the framework was very successful, as is.
Once I finished, however, I went back and made some improvements based on what I had learned.
Firstly, I incorporated Aristotle’s suggestion on View registration in the MVC pattern. That removed some of the more cumbersome code from the client. While it added extra calls to the View class, those calls were optional, and only have to be supported by game implementations that find the functionality useful. So the additional complexity was optional, and shouldn’t break the existing Alphametics code.
That was the biggest change, and it was a fairly minor one.
I also realised that I had copy-and-pasted a slab of code from the Alphametics solution. It wasn’t a large slab, but it was a complex one (dealing with PyGame events, and passing them on the the appropriate View object), so I was happy to factor it out, and add it into to a new subclass in the View.
I’m aware that these changes aren’t exactly riveting reading, but the conclusion I want
you to draw from that is that the framework did very well.
For what it is worth, there was about 300 lines of Python code (including comments and blank lines) in the Circuit Puzzle Model, 200 lines in the View and about 30 in the Controller.
Conclusion
Ummm… My conclusions were… errr… that I concluded that… ahhh… in light of this experience… let’s see…
Hooray for code re-use?
Comment by Aristotle Pagaltzis on September 17, 2008
Cole’s Law.
Comment by Julian on September 17, 2008
Coles’ Law; thinly sliced cabbage
Aristotle, are you really making a reference to an old joke? Perhaps you mean Kirchhoff’s First Law (which I guess, if you accept this is a electrical circuit, is the name of the constraint between cells)?
Comment by Jonathon Duerig on September 17, 2008
I played these circuit games for a couple of hours after your original article. During the course of that, I have come to an intuitive conclusion.
I don’t think that it is possible to have a grid with both a circuit and a tree solution. Now let me just think of how to prove it or provide a counterexample…
-D
Comment by Jonathon Duerig on September 17, 2008
After a little bit of thought, here is the outline of my intuition. Let us suppose that there is a tree solution. Then lets take an arbitrary non-terminal square as the root of that tree.
Every square except that root will have one edge connected to the root and the remainder connected elsewhere. A two-way will have one connected to the root and another connected ‘downstream’, so it doesn’t add any branching. A three-way will add an extra branch. A four-way will add two extra branches.
If the sum of these branching values is equal to the number of terminal squares, then only a tree solution is possible. This is because there are no free ‘edges’ that can connect with one another. If the branching values is greater than the number of terminal squares, then there must exist one or more circuits.
Not exactly rigorous, but convincing to me.
-D
Comment by Julian on September 17, 2008
Jonathon,
I haven’t given this enough thought, but I think there is an assumption in your reasoning that the solution is not disjoint.
If you permit disjoint solutions, I think you can get cycles.
(Just to be clear: While the Power-based puzzles don’t permit disjoint solutions, my code isn’t smart enough to know that. The question is whether that is an issue.)
The correct way to prove it is with a counter-example, and I think I have one. Give me a while to check my work and render it.
Comment by Jonathon Duerig on September 17, 2008
Ah. No need. I was indeed assuming that they couldn’t be disjoint. Here is a quick counterexample if they are disjoint:
***++*
*++*
LL
Where * is terminal, + is a 3-way, and L is a 2-way.
The tree solution has the three ways in each row facing away from each other. But if the bottom two three-ways face away from the top two three-ways instead, you have a disjoint graph which is also a cycle on the bottom. The ‘L’s always point towards each other and to the north.
-D
Comment by Julian on September 17, 2008
Too late